Hi pa...!
After a long hiatus, I am back...! :)
This time, I have decided to share another gem that was posed to a lit'l Ramanujan by a Math teacher at his school who had heard about his mathe-magical flair...!
[details may vary...I'm not exactly sure...but that's not important here..!]
Consider the below pair of equations :
Sqrt(x) + y = 7 ---> (1)
x + Sqrt(y) = 11 --->(2)
Look simple don't they..?? :)
They are deceptively like the 'simultaneous equations' in 2 unknowns viz., x & y that we all have known very well in school, right ?
Now, I request you to please grab a piece of paper, & really try solving fer x & y...& see for yourself..! :)
You will soon find that it's not so easy after all, with the brute-force method of eliminating either x or y only leading to more troubles..! Take my word fer it..!!
Hmmmmmmm...!!
Anyway, please do let me know of ANY elegant method(s) of solving this pair of equations that you may stumble upon, or KNOW already..!
The solution to the above pair...which is quite obvious, is : (x=9, & y=4)
What did lit'l Ramanujan do?--- you might ask...
Well, it is said he was ready with the answer in a jiffy ! :)
{But HOW did he approach it?? HOW did he crack it ??
I do not know; it's all shrouded in 'mist'ery...in his-story...! :)}
Love & Best Wishes,
The moRon in rags,
Planet Earth
============================================
And here's a point to ponder...! :)
"Obvious is the most dangerous word in mathematics."
- E.T. Bell
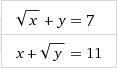

Anyway, the "normal", "formal" {But something i HATE...becoz it's NOT b'ful...! Too HARD..!! :-/ } way to solve this baby, is to see that,
ReplyDeletey = (11-x)^2,
& to put that into the equation :
x = (7-y)^2
=> x - ( 7-(11-x)^2) ^2 = 0
x^4 - 44x^3 + 712x^2 - 5017x + 12996 = 0
This, friends, is the correct equation to solve!
And luckily (x-9), is one of the factors..! :) i.e., the above equation can be factorized as :
(x-9)(x^3 - 35x^2 + 397x - 1444) = 0
Anyway, me discussing with some friends about another ridiculous way I've devised...! ;)
Will update you once/if that's confirmed..! :)
looking at the expression one can easily deduce that x , y >0.
ReplyDeleteWith that in place the second deduction wud be x,y would be perfect squares
With this try doing hit & trial & one wud end up with one result
I am a moron in Maths. I feel amazed when I see such problems.
ReplyDelete